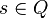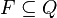后缀自动机入门
后缀自动机是一种接受所有后缀的DFA
寒假刚完后缀数组开始看 SAM , 结果发现这玩意一点也不好学
从一个题讲起:
最近SAM对字符串情有独钟. 给一字符串S, SAM想知道有一些单词是否是这个字符串的子串.
SAM觉得这个问题太过简单, 他定义了一种操作. 在字符串S末尾添加字符串c.
询问则是给出一个单词, 询问这个单词在当前字符串S中是否出现过(是否为子串)abcdef
5
2 abc
2 efg
1 g
2 efg
2 cdeYES
NO
YES
YES
如果不对字符串进行修改, 显然可以用 AC自动机 划水. 把所有询问模式串插入字典树, 建立AC自动机, 然后对文本串O(n)的匹配, 就可以统计出各个模式串是否出现.
然而有修改, 然而有修改, 然而有修改. 注意AC自动机本质上是对模式串建立一个快速匹配的自动机(快速匹配原理同kmp), 对于长度为n的文本串, 需要O(n)的扫描才能知道是否每个模式串是其子串.
这个题目却对文本串进行修改, 因此每次都需要O(n)复杂度才能进行判断是否出现.
如果有一种自动机可以匹配文本串的任意子串呢? 只需要让模式串在这个自动机上转移, 就可以得知是否为文本串的子串.
后缀自动机的定义
后缀自动机是一种DFA:
确定有限状态自动机 是由
是由
所组成的5-元组。因此一个DFA可以写成这样的形式: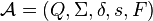 。
。
因为这个editor对行内mathjax的公式支持不是很友好. 接下来的记号说明:
SAM(T), 表示对字符串T建立的后缀自动机.
sigma, 表示字母表(例如全部小写英文字母)
trans, 表示转移函数, trans(p, x) = q 表示自动机上p状态经过字符x的转换到达状态q, trans(p, S) = q(其中S是一个字符串, s0s1s2...sn-1)表示trans…(trans(trans(p, s0), s1), …) = q
init, 表示自动机的初态
end, 表示自动机的终态集合, trans(init, S) in end即字符串S经过初态的转换被自动机接受, 被SAM(T)接受则表示S为T的一个后缀
L(p), 表示自动机SAM上状态p开始读入字符, 能接受的所有字符串. L(init)即SAM能接受的所有后缀
后缀自动机的建立
暴力
最蠢做法, 把字符串T的所有后缀插入 Trie树, 并建立 AC自动机. 在这个 AC自动机 上转移就可以满足需求.
然而..
|T| = n, 则空间复杂度为
O(n^2). 选择死亡..分析
显然我们需要一个状态数更少的后缀自动机.
考虑字符串 T, 其后缀构成的集合为 SFX , 连续子串集合 FAC
对于任何字符串 S, 如果
S not in FAC, 则trans(init, S) = null( S 无论如何转移也不可能变成后缀, 无须浪费空间)同时, 如果
S in FAC, 则 S 就有成为后缀的可能, 字符串在自动机上的匹配每次消耗一个字符, 进行一次转移, 因此 SAM(T) 需要识别所有子串(而不仅仅是所有后缀)我们不能对每个
S in FAC都新建一个状态, 因为|FAC|太大. 考虑trans(init, S)能识别哪些字符串, 即L(trans(init, S)). 而x in L(trans(init, S))当且仅当Sx in SFX, 因为我们已经读入 S.对于一个状态 p , 我们关心的是 L(p).
如果
Sa = S[l:r], 则trans(init, Sa)开始能识别从 r 开始的后缀.例如 Sa 在 S 中出现位置集合为
{[l1, r1), [l2, r2), … [ln, rn)},那么
L(trans(init, Sa)) = {S[r1:], S[r2:], … S[rn:]}. 令Right(Sa)={r1, r2, …, rn}, 则L(trans(init, Sa))与Right(Sa)等效那么对于两个子串 Sa, Sb. 若
Right(Sa)=Right(Sb), 则L(trans(init, Sa))=L(trans(init, Sb)), 则trans(init, Sa), trans(init, Sb)完全可以归入同一个状态容易知道
Right(S)等价的所有 Sx 长度为一个连续的区间.(自己想), 不妨令这个区间为[Min(S), Max(S)]考虑两个状态 a, b. 他们表示的 Right 集合为 Ra, Rb. 假设 Ra 与 Rb 有交集, 设
r in Ra & Rb. 状态 a 表示的子串和状态 b 的子串不会有交集(因为trans(init, Sx)是一个确定的状态),所以
[Min(a), Max(a)]和[Min(b), Max(b)]不会有交集(如果有交集, 则他们存在相同子串, 矛盾). 不妨设Max(a) < Min(b), 有 a 表示的串均为 b 表示的串的后缀. 因此 Rb 是 Ra 的真子集(clj的ppt好像写反了?)那么任意两个状态对应的 Right 集合, 要么不相交, 要么一个是另一个的真子集
这个性质很重要.. 说明 Right 集合构成一个树形结构, 而且叶子节点至多 N 个, 如果
fa = parent(s), 则Max(fa) = Min(s) - 1叶子节点至多N个, 同时每个节点至少2个孩子, 可以得知这个数的节点数是
O(n)的(Why?)边数也是
O(n)的, 对N个节点建立生成树, 对于不在生成树上的边trans(p, x)=q, 一定存在init->p, p->q, q->终态的路径, 即对应一个确定的后缀. 而字符串的后缀数目是O(n)的, 因此非树边也是O(n)的.Right 集合构成的树形结构叫 Parent 树,
fa = parent(s), 则 fa 状态的 Right 集合是包含s状态的 Right 集合的元素最少的集合.如果有
trans(x1, c1) = trans(x2, c2)……=trans(xk, ck) = x,则c1 = c2 …… = ck!且状态x1, x2, ……xk在 parent 树中构成一段连续的 Parent 链(即有父子关系)。链的最底部最小的儿子为 xi,当且仅当step[xi] + 1 = step[x]
构造
经过上面的分析. 下面给出在线, 线性的构造SAM的方法.
每读入一个字符 x, 更新当前字符串 T 的 SAM(T) 为新字符串 Tx 的SAM(Tx).
考虑 SAM(T) 和 SAM(Tx) 的差别, 前者可以接受所有T的后缀, 识别所有T的子串, 显然后者能识别的子串除了T的所有子串, 还有Tx的后缀.
这只是状态转移的合法性, 但是在之前的分析中, 为了压缩状态, 我们将一个状态和 Right 集合对应起来, 并用 Parent 树记录这种 Right 集合的真子集关系.
因此从 SAM(T) 到 SAM(Tx), 需要保持两种性质
- 转移合法性: 接收 Tx 的所有后缀,且保证Tx的所有子串有合法转移( trans 的更新)
- 状态法性:每个状态和新增状态的 right 集满足定义,即:转移到同一个状态的所有子串有相同的 Right 集。(涉及 Parent 链的更新)
对于(1),因为 Tx 的子串 = T 的所有子串+ Tx 的所有后缀,因此我们只需要保证 Tx 的所有后缀有合法转移就行!而 Tx 的后缀完全是由T的所有后缀增加一个字符 x 得来的,我们只需要挨个找出 T 的后缀在 SAM(T) 中的状态,然后再保证这些状态在 SAM(Tx) 当中有 x 转移, 并转移到终态即可.
首先增加一个 np 节点.
如何查找 SAM(T) 对应的终态? (沿着 Parent 树从
Right={|T|}向上查一条链, 他们都是终态)设SAM(T)当中后缀对应的终态=
{v1, v2, …….vk},回溯的时候会出现哪些情况呢?trans(p, x) = null,即不存在 x 转移,我们就必须增加一个 x 转移 SAM(Tx) 的终点 np 即可,同时保证了性质(2);q = trans(p, x) != null很好嘛,已经有 x 转移了,我们只需要保持性质(2)就行。扩充Right(q),即把 np 的 parent 的指针链向 q 不就 ok 了嘛!
然而有错, 然而有错, 然而有错.
假设 p 是沿着 parent 链查找时遇到的第一个有 x 转换的节点.那么 p 沿着 parent 链继续向上查找的节点也都有 x 转换(因为在 parent 链上走的过程是 Right 集合增大的过程)
考虑前面的性质,
trans(p, x) = q, 一定存在p1, p2, …, pm满足trans(pi, x) = q. 并且p1-pm在 parent 树中为一条链, 假设 p1 为链底端状态, 即parent(p1) = p2, parent(p2) = p3, …当
p == p1, 好像没有什么不对, 只需要把 np 的 parent 指向 p 即可, 因为p1, p2, …, pm都是 SAM(T) 的终态(由于 parent 链)当
p!=p1, 假设p==pk, 则p1, p2, …, pk-1并非 SAM(T) 的终态. 如果此时只是简单的parent(np) = q, 后果是通过p1, p2, … pk-1经过 x 字符转换到达状态 q, 其实不应该是 Tx 的后缀, 而 q 的 Right 集合里包含了 np 的 Right 集合(这意味着 q 是 SAM(Tx) 的终态). 对于通过pk, pk+1, …, pm经过字符x转换达到状态 q 的字符串, 他们又确实是 Tx 的后缀(因为pk, pk+1, …, pm是 SAM(T) 的终态, 因此他们本来是T的后缀, 添加字符x之后显然是 Tx 的后缀).怎么解决这个问题?
办法也很简单, pk 将
p1, p2, …, pm分成了两部分,{p1, …, pk-1}经过 x 转换之后到达的状态不应该是终态,{pk, …, pm}经过x转换之后到达的状态应该是终态. 只需要把 q 节点复制, 成为 nq 节点. 对于{p1, …, pk-1}, 不修改他们, 也不让parent(np)指向 q, 而对于{pk, …, pm}, 让他们经过 x 转换后到达状态 nq , 同时parent(np)指向 nq.这就构造出了 SAM(Tx).
复杂度粗略估计是线性的, 因为每次都在添加parent边和trans边, 而最终的自动机中边数是
O(n)的.实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
int len;
struct SAM{
struct SNode{
int step;
int next[SIGMA_SIZE];
int fail;
}node[MAXN<<1];
int scnt, end;
SAM() : scnt(0){}
void init(){
scnt = 0;
end = newNode(0);
}
int newNode(int step){
node[scnt].step = step; node[scnt].fail=-1;
memset(node[scnt].next, -1, sizeof(node[0].next));
return scnt++;
}
void insert(char c){
int x = c-'a';
int p = end;
int np = newNode(node[p].step+1);
while(p>=0 && node[p].next[x] == -1)
node[p].next[x] = np, p = node[p].fail;
if(p == -1)
node[np].fail = 0;
else{
int q = node[p].next[x];
if(node[p].step+1 == node[q].step)
node[np].fail = q;
else{
int nq = newNode(node[p].step+1);
memcpy(node[nq].next, node[q].next, sizeof(node[0].next));
node[nq].fail = node[q].fail;
node[q].fail = nq;
node[np].fail = nq;
while(p>=0 && node[p].next[x] == q)
node[p].next[x] = nq, p = node[p].fail;
}
}
end = np;
}
void build(char *s){
int len = strlen(s);
init();
for(int i=0; i<len; i++)
insert(s[i]);
}其实代码很短..

 (非空有限的字符集合)
(非空有限的字符集合)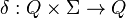 (例如:
(例如: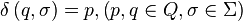 )
)